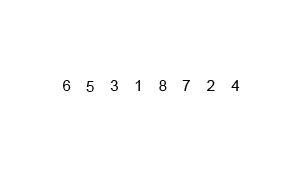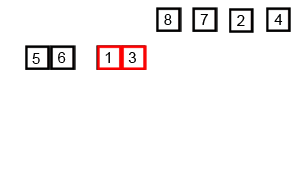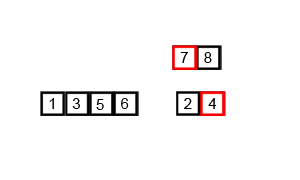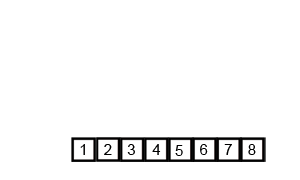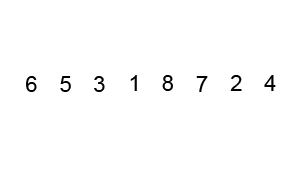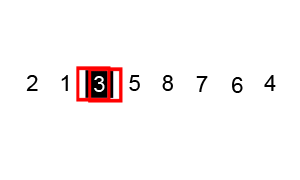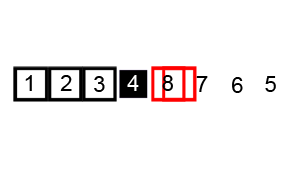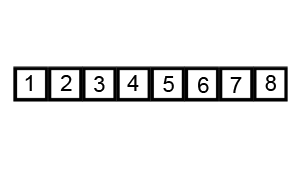CIS 115

Algorithms

al-Khwārizmī

Abū ʿAbdallāh Muḥammad ibn Mūsā al-Khwārizmī

Image Source: Wikipedia

Algorithm

A finite list of specific instructions for carrying out a procedure or solving a problem

Euclid

Image Source: Wikipedia

Euclid's Algorithm (GCD)

1. Start with 2 numbers, A and B
2. If either one is zero, the answer is the other number
3. Subtract the smaller number from the larger number
4. Repeat steps 2 - 4 until an answer is found

Example: GCD of 1071 & 462

Example: GCD of 1071 & 462

• 1071, 462
• 609, 462
• 147, 462
• 147, 315
• 147, 168
• 147, 21
• 126, 21
• 105, 21
• 84, 21
• 63, 21
• 42, 21
• 21, 21
• 21, 0
• 21

Sorting Algorithms

• Insertion Sort
• Bubble Sort
• Merge Sort
• Quicksort

Insertion Sort

Image Source: Wikipedia

1. Choose an element from the source
2. Place it in the correct place in the destination
3. Repeat until source is emtpy

Bubble Sort

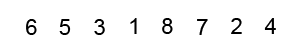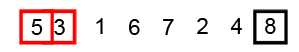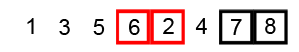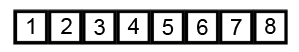
Image Source: Wikipedia

1. Compare the first two elements
2. If they are out order, swap them
3. Move one element over and repeat
4. When the end is reached, start over
5. Continue until no more swaps are made

Big O Notation

Image Source: Wikipedia

Big O Notation

• A way to express the complexity of an algorithm
• Approximates the number of steps needed based on the size of the input
• Assumes the input is a "worst case" input

Bubble Sort - Worst Case?

• 3, 2, 5, 4, 7, 6, 9, 8, J, 10, K, Q, A
• A, 2, K, 3, Q, 4, J, 5, 10, 6, 9, 7, 8
• A, Q, K, 10, J, 8, 9, 6, 7, 4, 5, 3, 2
• A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2
• 2, 4, 6, 8, 10, Q, A, 3, 5, 7, 9, J, K

Bubble Sort - Worst Case?

• 3, 2, 5, 4, 7, 6, 9, 8, J, 10, K, Q, A - 6
• A, 2, K, 3, Q, 4, J, 5, 10, 6, 9, 7, 8 - 42
• A, Q, K, 10, J, 8, 9, 6, 7, 4, 5, 3, 2 - 73
• A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2 - 78
• 2, 4, 6, 8, 10, Q, A, 3, 5, 7, 9, J, K - 21

Bubble Sort - Worst Case?

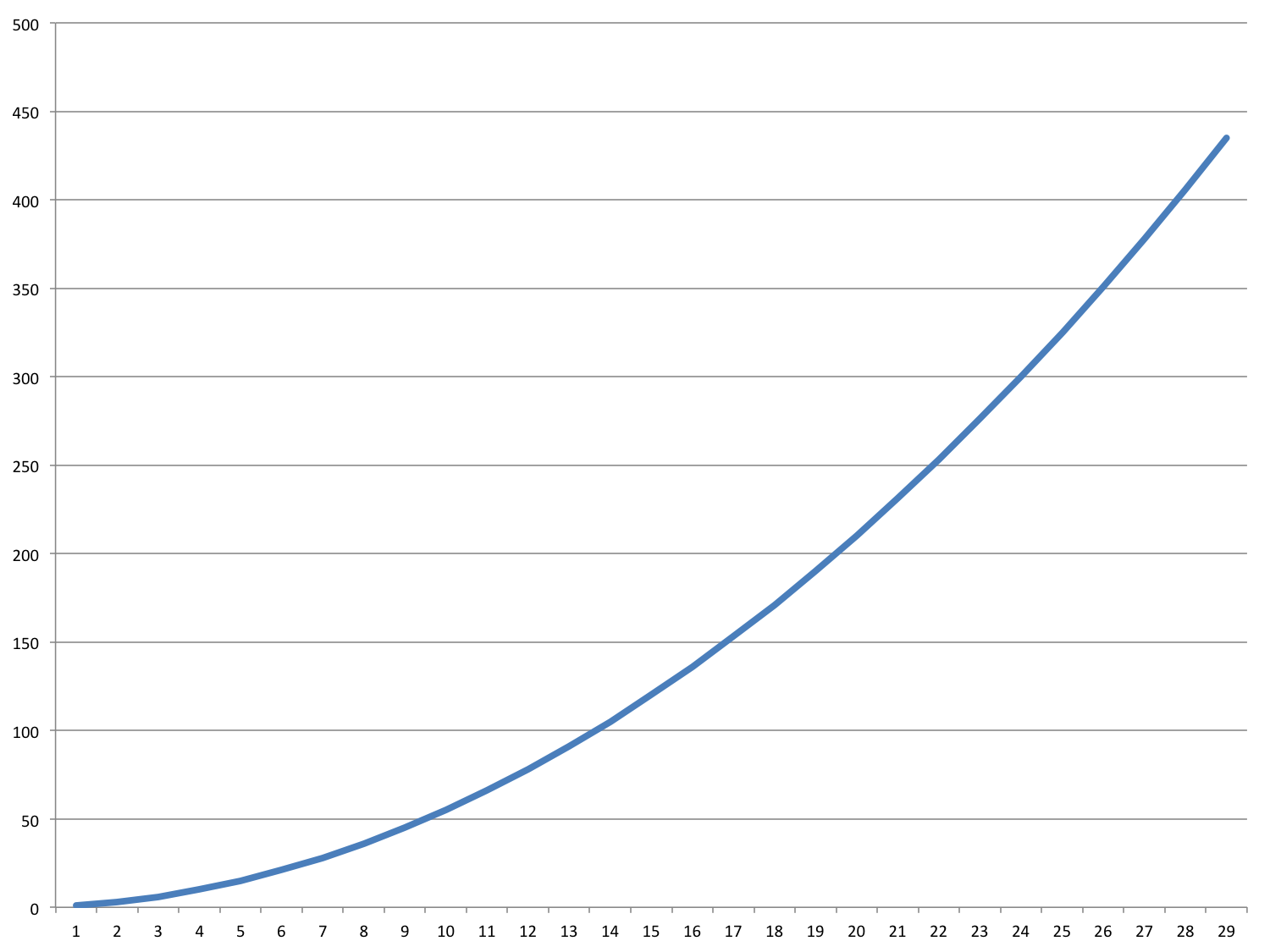
Sorting Algorithms

• Insertion Sort - O(n²)
• Bubble Sort - O(n²)
• Merge Sort
• Quicksort

Merge Sort

Image Source: Wikipedia

Merge Sort

1. Split the items into two halves
2. Repeat step 1 until each has 1 item
3. Choose 2 parts and merge them together by choosing the smallest item repeatedly from the front of each part
4. Continue merging parts together until no more remain

Quicksort

Image Source: Wikipedia

Quicksort

1. Choose an item from the list as a "pivot"
2. Put all items less than that item to its left, and put all items greater to its right
3. Repeat these steps for the items on each side of the pivot.

Sorting Algorithms

• Insertion Sort - O(n²)
• Bubble Sort - O(n²)
• Merge Sort - O(n log n)
• Quicksort - O(n²) - avg. O(n log n)

Everyday Heuristics

• Rule of Thumb
• Educated Guess
• Common Sense
• Try something and work backwards
• Do a simpler problem first

Traveling Salesman Problem

Image Source: Wikipedia

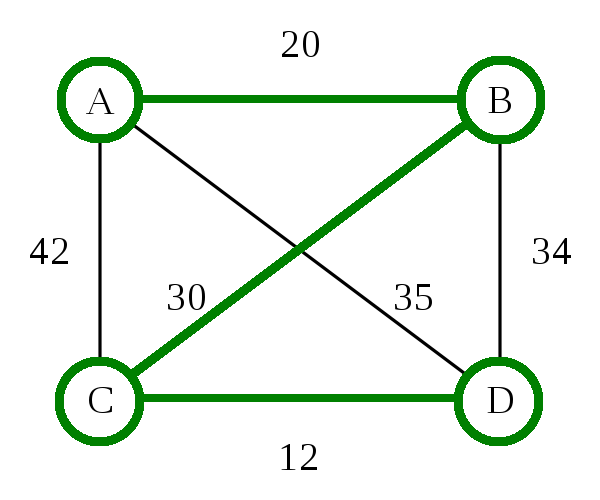
Traveling Salesman Problem: Algorithms

• Brute Force - O(n!)
  • Easy & Cheap, but not fast
  • 8 cities = 40320 steps
• Dynamic Programming - O(2ⁿ)
  • Faster, but not easy or cheap
  • 8 cities = 256 steps

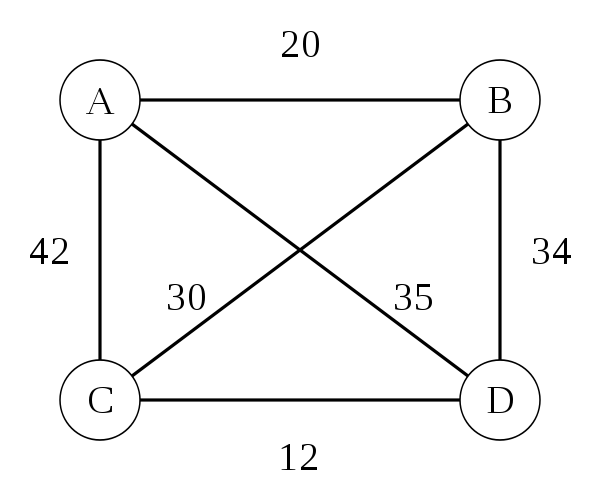
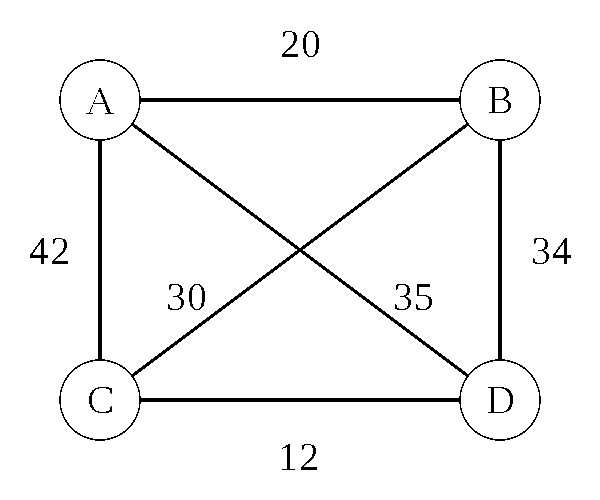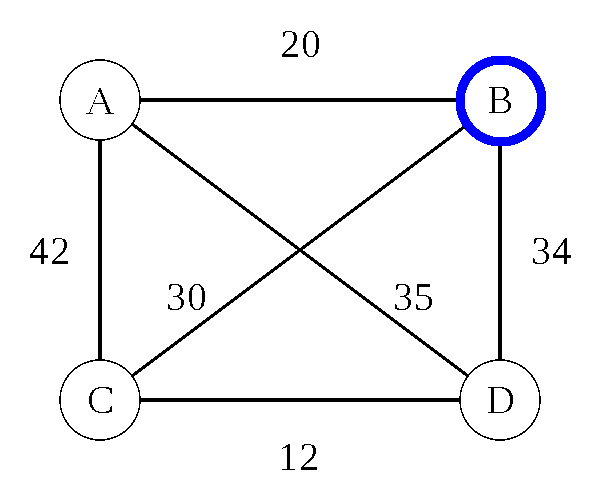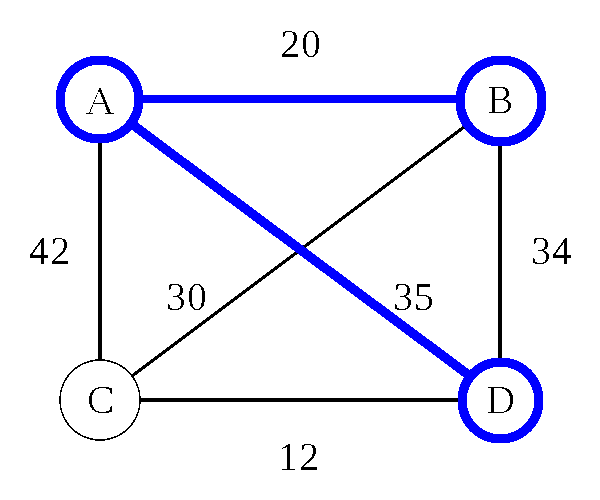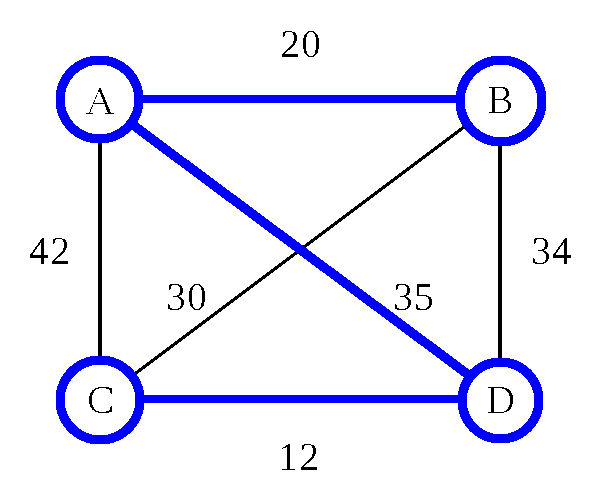
Traveling Salesman Problem: Heuristic

Nearest Neighbor (Greedy Algorithm)

• Pick any city (we'll use B)
• Go to the closest city you haven't been to yet
• From that city, repeat this process until all cities have been visited

Traveling Salesman Problem

Greedy Solution: 67 miles

Image Source: Wikipedia

Traveling Salesman Problem

Optimal Solution: 62 miles

Image Source: Wikipedia

Traveling Salesman Problem: Heuristic

Nearest Neighbor (Greedy Algorithm) - O(d n)

• d is the number of dimensions
• n is the number of cities
• 8 cities = 16 steps (assuming 2D maps)

Time can vary widely based on how the data is presented and sorted

Assignments

• Read and be prepared to discuss:
  • Pattern on the Stone Chapter 6: Memory: Information and Secret Codes
• Blog 2: Algorithms -
  Due Monday 2/15 10:00 PM
• Scratch Sorting Project -
  Due 2/16 10:00 PM

Blog 2: Algorithms

There are many important algorithms in Computing Science. In fact, we’re going to learn about many of them later in this class. For now, however, I’d like you to pick an algorithm from Wikipedia’s list of algorithms (https://en.wikipedia.org/wiki/List_of_algorithms) and write about it. Some things you can cover:

• Where did this algorithm come from?
• How does it work?
• What makes it special or unique?
• Are there other algorithms that achieve the same or similar outcome?
• Could you do this algorithm manually? Or does it require a computer?
• How does this algorithm relate to what we’ve already read in the textbook? Did the textbook help you understand how this algorithm works? (textbook references)
• Where can this algorithm be found in the real world? (outside reference)

Bubble Sort

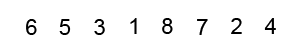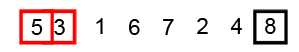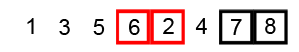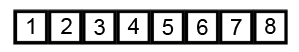
Image Source: Wikipedia

1. Compare the first two elements
2. If they are out order, swap them
3. Move one element over and repeat
4. When the end is reached, start over
5. Repeat these steps as many times as the number of items in the list