CIS 115 - Bits and Boolean Algebra

CIS 115

Bits and Boolean Algebra

Red Green - Boolean Logic on YouTube

Aristotle

Image Source: Wikipedia

Aristotelian Logic

Premise:
All men are mortal
Socrates is a man
Conclusion:
Therefore, Socrates is mortal

George Boole

Image Source: Wikipedia

The Laws of Thought

Image Source: Project Gutenberg

Boolean Logic

Premise:
A ∧ B
B ∧ C
Conclusion:
A ∧ C

Note: This translation is somewhat flawed, but I'll leave that to a later course in logic or philosophy to describe why.

Boolean Symbols

∧  &&

∨  ||

⊕

¬  !

And

A ∧ B

Image Source: Wikipedia

A ∧ B ∧ C

Image Source: Wikipedia

A ∨ B

Image Source: Wikipedia

A ∨ B ∨ C

Image Source: Wikipedia

Exclusive Or (XOR)

A ⊕ B

Image Source: Wikipedia

A ⊕ B ⊕ C

Image Source: Wikipedia

Not

¬ A

¬ B

Image Source: Wikipedia

¬ B

Image Source: Wikipedia

Augustus De Morgan

Image Source: Wikipedia

De Morgan's Law

Negation (inverse) of a logic statement

¬ ( A ∧ B ) = ( ¬ A ) ∨ ( ¬ B)

¬ ( A ∨ B ) = ( ¬ A ) ∧ ( ¬ B)

Distribute the negative (¬) then swap ands (∧) and ors (∨)

Boolean Algebra

∨ works like addition ( + )
¬ works like negation ( − )
∧ works like multiplication ( × )
Associative: (A ∧ B) ∧ C = A ∧ (B ∧ C)
Commutative: (A ∧ B) = (B ∧ A)
Distributive:
A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C)

Logic via Electrical Switches?
Charles Sanders Peirce

Image Source: Wikipedia

Claude Shannon

Image Source: Wikipedia

A Symbolic Analysis of Relay and Switching Circuits

Image Source: MIT

"...possibly the most important, and also the most famous, master's thesis of the century."
- Psychologist Howard Gardner (via Wikipedia)

Logic Gates

AND	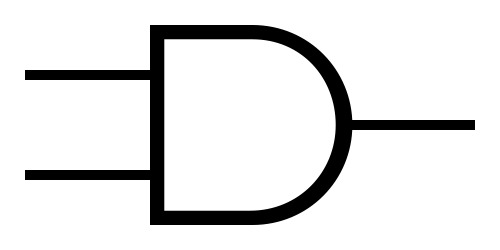OR	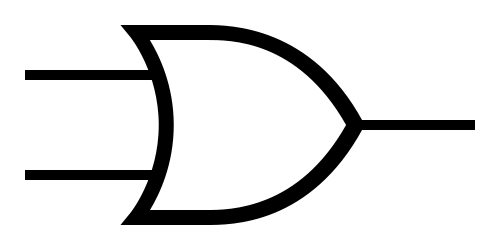XOR	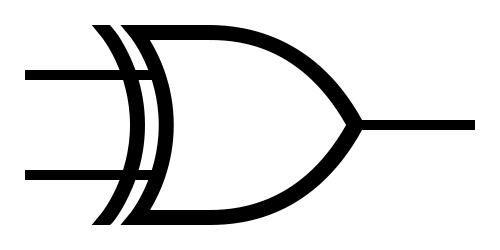NOT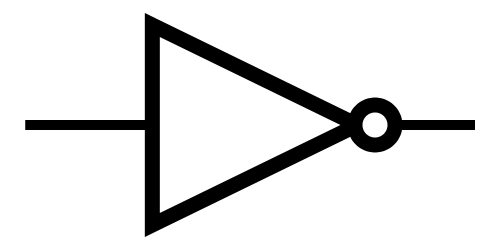

NAND	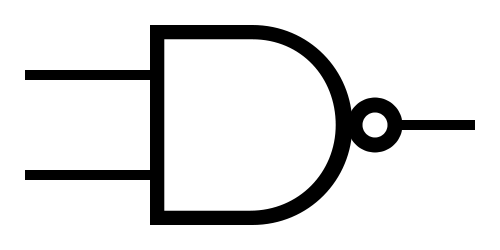NOR	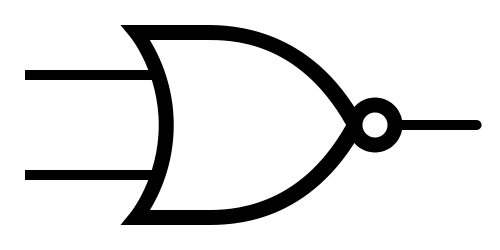XNOR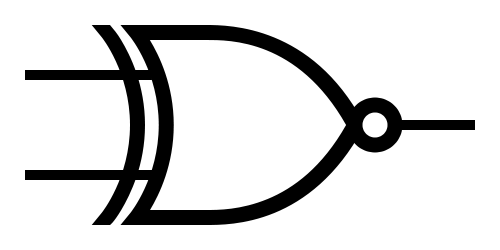

Note: The little circle at the end of the NOT gate is the only part that matters.

Boolean Values

Boolean	Binary	Electrical
TRUE	1	ON
FALSE	0	OFF

Note: These values are traditionally used in theory. In many electronic systems and programming languages these values may be reversed for various reasons. Check the manual!

Example 1

A	B	C	OUT
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

(A ∧ C) ∨ (B ∧ C)

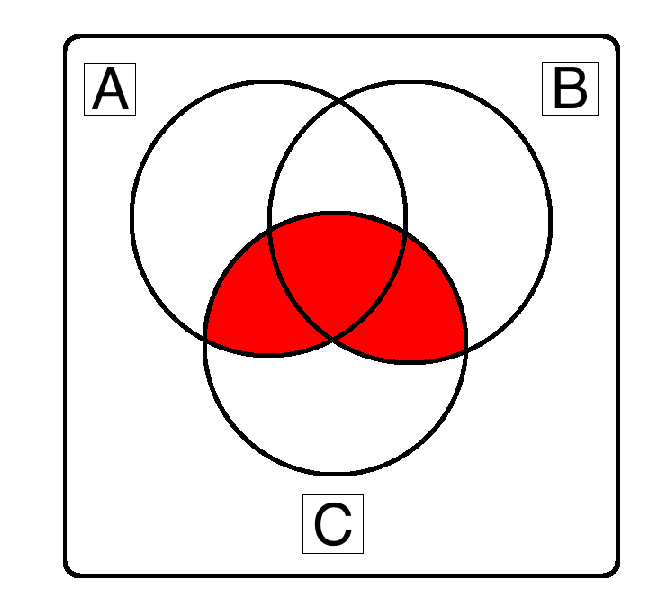
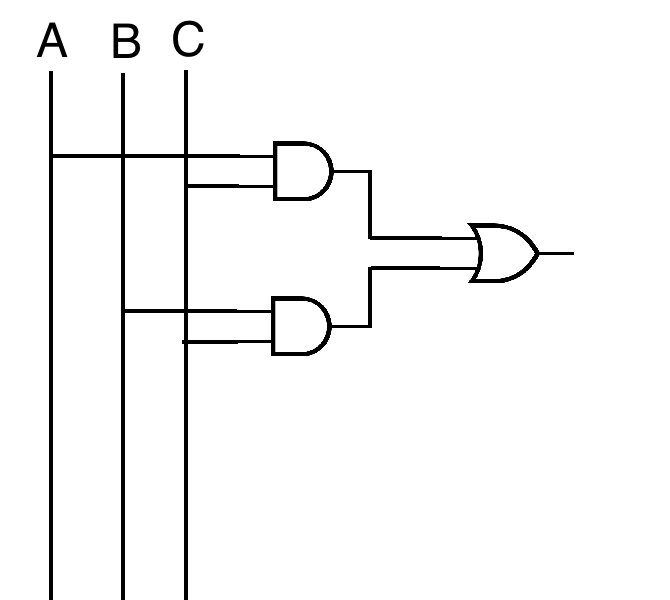
C ∧ (A ∨ B) works as well

Example 2

A	B	C	OUT
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

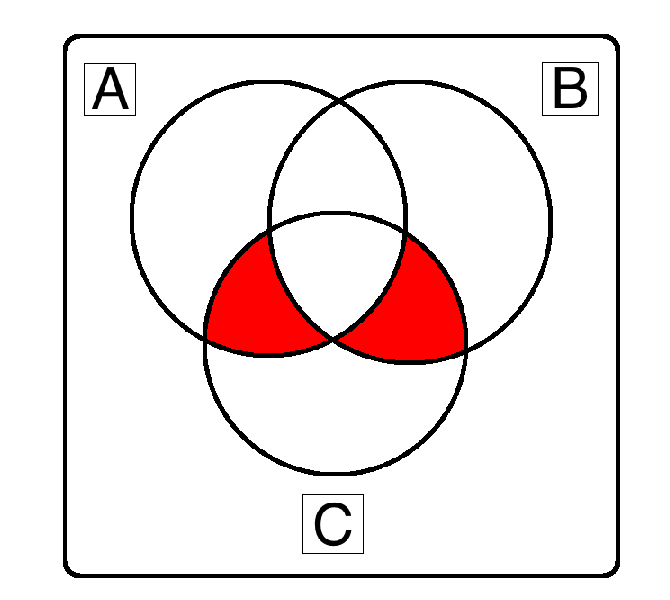
¬A ∧ ( B ∨ C )

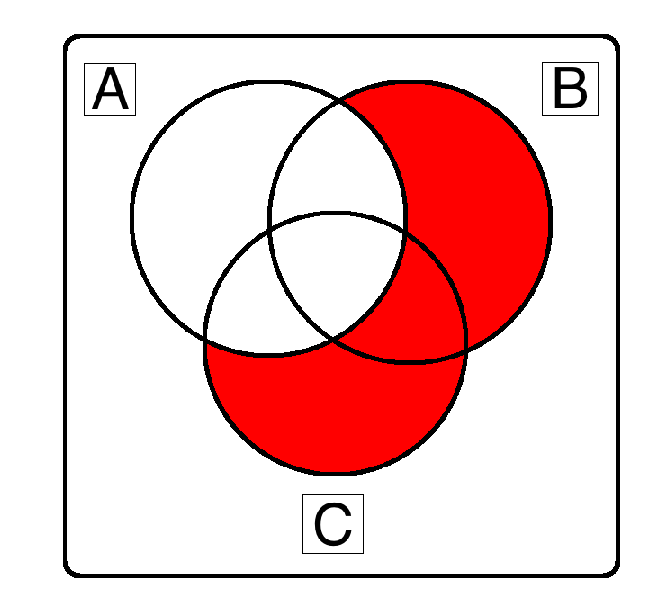
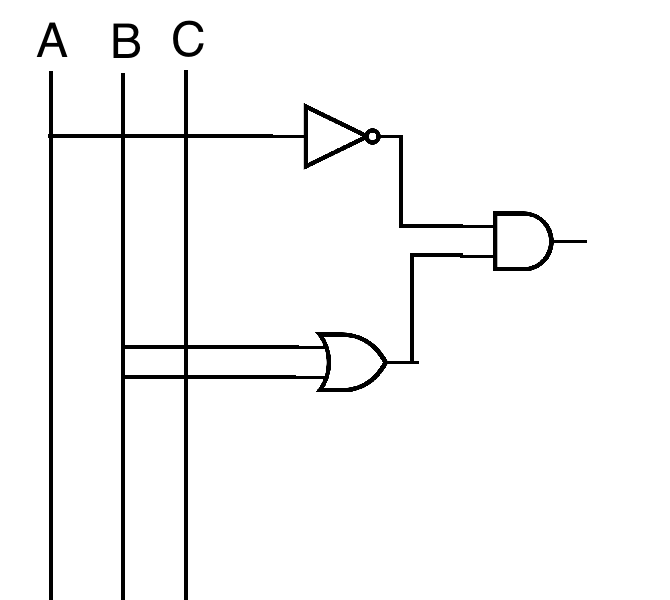
( ¬A ∧ B) ∨ ( ¬A ∧ C) works as well

Example 3

A	B	C	OUT
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

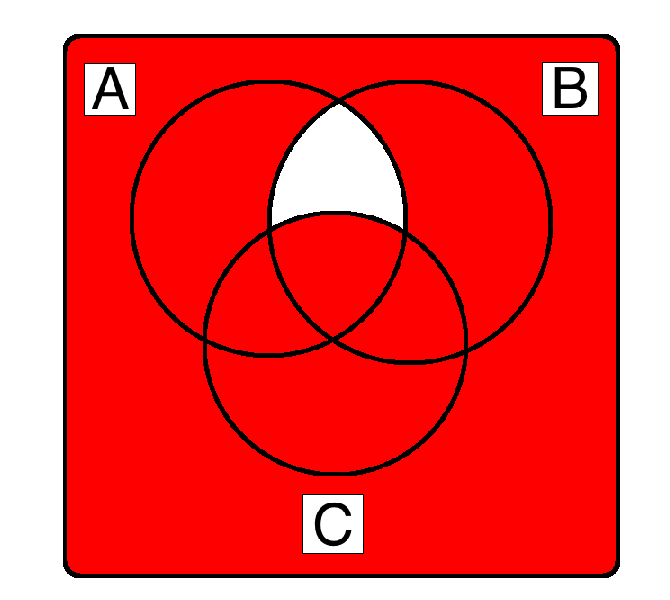
( A ⊕ B ) ∧ C

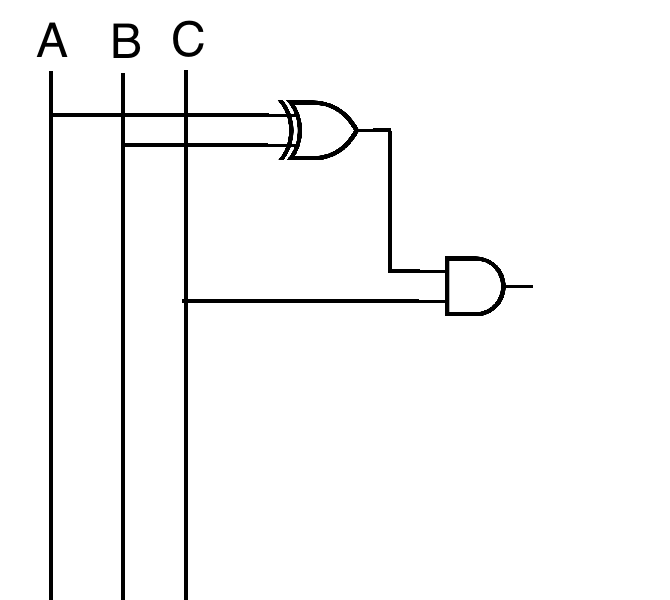
(A ∧ C) ⊕ (B ∧ C) works

(A ∧ ¬B ∧ C) ∨ (¬A ∧ B ∧ C) works

Example 4

A	B	C	OUT
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

¬ ( A ∧ B ∧ ¬C )

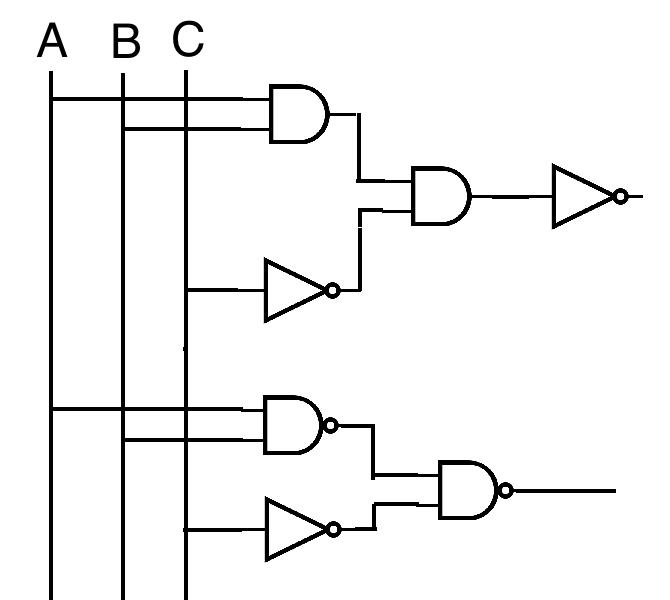
By De Morgan's Law
( ¬A ∨ ¬B ∨ C ) works as well

Universal Logic Gates

Image Source: Wikipedia

Universal Logic Gates - Adder

Image Source: Wikipedia

Image Source: schoolphysics.co.uk

Next Steps

Programming
Finite State Machines

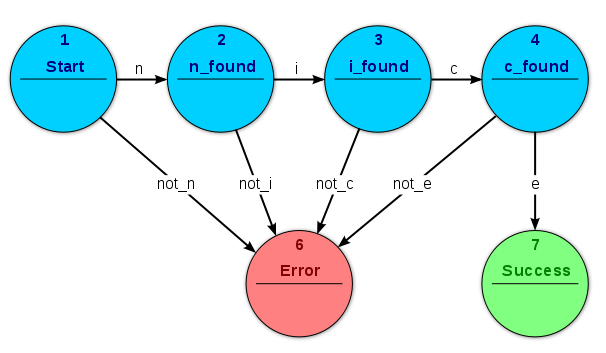
Image Source: Wikipedia

Assignments

Read and be prepared to discuss:
- Pattern on the Stone
  Chapter 3: Programming
Blog 1: Personal Biography - Due Monday 2/1 10PM
Scratch Project 1 - Due 2/9 10PM

Blog 1: Personal Biography

Tell us a little about yourself. This is your chance to let us know who you are and what interests you. Some questions you can answer to get you started are below, but feel free to be as creative and expressive as possible introducing yourself.