CIS 115
Lecture 8: Encoding Data
Binary - Natural Numbers
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0*128 | 0*64 | 1*32 | 0*16 | 1*8 | 0*4 | 1*2 | 0*1 |
32 + 8 + 2 = 42
Binary Data Types
- Unsigned Integer (Natural Number)
- Signed Integer
- Float
Negative Numbers
- One's Compliment - Just invert the bits
- Sign Bit: 0 is positive, 1 is negative
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
Negative Numbers
- One's Compliment - Just invert the bits
- Sign Bit: 0 is positive, 1 is negative
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | -42 |
One's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | -42 |
=
One's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | -42 |
=
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -0 |
Hmm, that's not quite right...
Negative Numbers
- Two's Compliment -
Invert the bits and add 1
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
invert
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Negative Numbers
- Two's Compliment -
Invert the bits and add 1
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
invert
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
plus 1
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | -42 |
Two's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | -42 |
=
Two's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | -42 |
=
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
That works!
Other Values
| Binary | Unsigned | Signed |
| 00000000 | 0 | 0 |
| 00000001 | 1 | 1 |
| 00000010 | 2 | 2 |
| 01111110 | 126 | 126 |
| 01111111 | 127 | 127 |
| 10000000 | 128 | -128 |
| 10000001 | 129 | -127 |
| 10000010 | 130 | -126 |
| 11111110 | 254 | -2 |
| 11111111 | 255 | -1 |
Range of Values
- 8 Bit numbers
- Unsigned: 0 → 28 - 1
- Signed: -(27) → 27 - 1
- General Numbers - n bits
- Unsigned: 0 → 2n - 1
- Signed: -(2n-1) → 2n-1 - 1
Rational Numbers
The decimal point can "float" around

Floating Point
- IEEE 754 Standard - 16 bits (Half)
- The exponent has a bias of 15
- The leading one of the mantissa is implied
| - | Exponent | Mantissa | |||||||||||||
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Floating Point Example
| - | Exponent | Mantissa | |||||||||||||
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Mantissa: (1).01010 = 1.3125
Exponent: 10100 - 01111 = 20 - 15 = 5
Floating Point Example
| - | Exponent | Mantissa | |||||||||||||
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Mantissa: (1).01010 = 1.3125
Exponent: 10100 - 01111 = 20 - 15 = 5
Value: 1.3125 * 25 = 42
1.01010 * 25 = 101010 = 42
Range of Values
- -65504 → +65504
- 5.96046 x 10-8 : minimum positive
- 0 11111 0000000000 = infinity
- 1 11111 0000000000 = -infinity
- 0 01101 0101010101 ≈ 0.33325 ≈ 1/3
Not exact, but not bad either
Real World
- Integer - 32 bits
- Long Integer - 64 bits
- Half - 16 bits (5 + 10)
- Float (Single) - 32 bits (8 + 23)
- Double - 64 bits (11 + 52)
Text - ASCII
011001100110111101110010011101000111
100100100000011101000111011101101111
Text - ASCII
011001100110111101110010011101000111
100100100000011101000111011101101111
- 01100110 (102)
- 01101111 (111)
- 01110010 (114)
- 01110100 (116)
- 01111001 (121)
- 00100000 (32)
- 01110100 (116)
- 01110111 (119)
- 01101111 (111)
Text - ASCII
011001100110111101110010011101000111
100100100000011101000111011101101111
- 01100110 (102) - f
- 01101111 (111) - o
- 01110010 (114) - r
- 01110100 (116) - t
- 01111001 (121) - y
- 00100000 (32) - sp
- 01110100 (116) - t
- 01110111 (119) - w
- 01101111 (111) - o
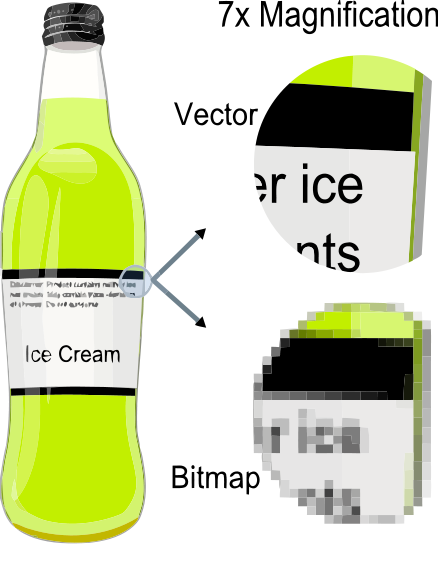
Vector Graphics (SVG)
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="350pt" height="450pt"
viewBox="0 0 350 450" version="1.1"
xmlns="http://www.w3.org/2000/svg">
<path fill="#ffffff" d=" M 0.00 0.00 L 270.80
0.00 C 270.29 1.10 269.84 2.22 269.41 3.34 C
270.05 3.42 271.34 3.57 271.98 3.65 C 271.83
2.43 271.66 1.21 271.49 0.00 L 320.83 0.00 C
320.62 1.16 320.43 2.32 320.27 3.48 C 320.88
3.49 322.11 3.50 322.73 3.51 C 322.60 2.64
322.35 0.89 322.23 0.01....
Compression
How much wood could
a woodchuck chuck if a
woodchuck could chuck wood?
Compression
How much wood could
a woodchuck chuck if a
woodchuck could chuck wood?
wood = 1 could = 2 chuck = 3
Compression
How much wood could
a woodchuck chuck if a
woodchuck could chuck wood?
wood = 1 could = 2 chuck = 3
How much 1 2 a 13 3 if a 13 2 3 1?
Assignments
- Read and be prepared to discuss:
- Pattern on the Stone Chapter 7: Speed: Parallel Computers
- Blog 3: Algorithms - Due 2/16 10:00 PM
- Scratch Sorting Project - Due 2/17 10:00 PM
Blog 3: Algorithms
Think about something that you do every day. That one thing probably is composed of many smaller steps, which you have to perform in the correct order. How would you describe those steps to someone unfamiliar with the action? How would you describe them to a robot that can follow your actions? While we may not think of it in this way very often, most of our daily lives could be expressed as an algorithm. Choose a few examples of actions you perform often, and write about how you would express them as algorithms. Some things to consider:
- Could a computer system be built to follow this algorithm easily?
- Are there algorithms you perform daily that would be very difficult for a computer?
- Is the algorithm you use the fastest one? Are there real-world limitations that prevent you from doing it faster?
- If the algorithm you use the most efficient one (the least number of steps) or simply the one that you learned first?
- How do you share your “algorithms” with others so they can follow along?
Binary Worksheet