CIS 115
Encoding Data
Binary - Natural Numbers
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0*128 | 0*64 | 1*32 | 0*16 | 1*8 | 0*4 | 1*2 | 0*1 |
32 + 8 + 2 = 42
Binary Data Types
- Unsigned Integer (Natural Number)
- Signed Integer
- Float
Negative Numbers
- One's Compliment - Just invert the bits
- Sign Bit: 0 is positive, 1 is negative
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
Negative Numbers
- One's Compliment - Just invert the bits
- Sign Bit: 0 is positive, 1 is negative
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | -42 |
One's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | -42 |
=
One's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | -42 |
=
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -0 |
Hmm, that's not quite right...
Negative Numbers
- Two's Compliment -
Invert the bits and add 1
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
invert
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Negative Numbers
- Two's Compliment -
Invert the bits and add 1
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
invert
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
plus 1
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | -42 |
Two's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | -42 |
=
Two's Compliment Addition
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
+
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | -42 |
=
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
That works!
Other Values
| Binary | Unsigned | Signed |
| 00000000 | 0 | 0 |
| 00000001 | 1 | 1 |
| 00000010 | 2 | 2 |
| 01111110 | 126 | 126 |
| 01111111 | 127 | 127 |
| 10000000 | 128 | -128 |
| 10000001 | 129 | -127 |
| 10000010 | 130 | -126 |
| 11111110 | 254 | -2 |
| 11111111 | 255 | -1 |
Range of Values
- 8 Bit numbers
- Unsigned: 0 → 28 - 1
- Signed: -(27) → 27 - 1
- General Numbers - n bits
- Unsigned: 0 → 2n - 1
- Signed: -(2n-1) → 2n-1 - 1
Rational Numbers
The decimal point can "float" around

Floating Point
- IEEE 754 Standard - 16 bits (Half)
- The exponent has a bias of 15
- The leading one of the mantissa is implied
| - | Exponent | Mantissa | |||||||||||||
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Floating Point Example
| - | Exponent | Mantissa | |||||||||||||
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Mantissa: (1).01010 = 1.3125
Exponent: 10100 - 01111 = 20 - 15 = 5
Floating Point Example
| - | Exponent | Mantissa | |||||||||||||
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Mantissa: (1).01010 = 1.3125
Exponent: 10100 - 01111 = 20 - 15 = 5
Value: 1.3125 * 25 = 42
1.01010 * 25 = 101010 = 42
Range of Values
- -65504 → +65504
- 5.96046 x 10-8 : minimum positive
- 0 11111 0000000000 = infinity
- 1 11111 0000000000 = -infinity
- 0 01101 0101010101 ≈ 0.33325 ≈ 1/3
Not exact, but not bad either
Real World
- Integer - 32 bits
- Long Integer - 64 bits
- Half - 16 bits (5 + 10)
- Float (Single) - 32 bits (8 + 23)
- Double - 64 bits (11 + 52)
Text - ASCII
011001100110111101110010011101000111
100100100000011101000111011101101111
Text - ASCII
011001100110111101110010011101000111
100100100000011101000111011101101111
- 01100110 (102)
- 01101111 (111)
- 01110010 (114)
- 01110100 (116)
- 01111001 (121)
- 00100000 (32)
- 01110100 (116)
- 01110111 (119)
- 01101111 (111)
Text - ASCII
011001100110111101110010011101000111
100100100000011101000111011101101111
- 01100110 (102) - f
- 01101111 (111) - o
- 01110010 (114) - r
- 01110100 (116) - t
- 01111001 (121) - y
- 00100000 (32) - sp
- 01110100 (116) - t
- 01110111 (119) - w
- 01101111 (111) - o
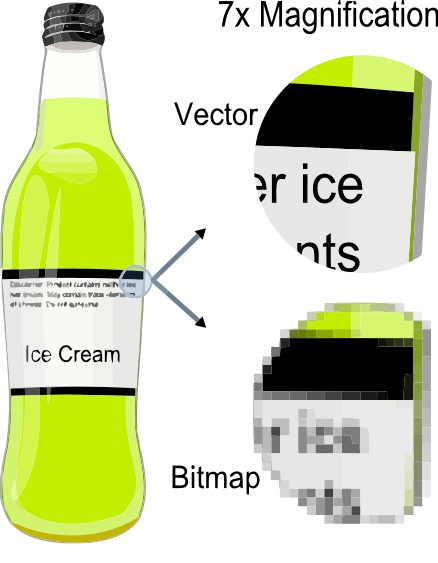
Vector Graphics (SVG)
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="350pt" height="450pt"
viewBox="0 0 350 450" version="1.1"
xmlns="http://www.w3.org/2000/svg">
<path fill="#ffffff" d=" M 0.00 0.00 L 270.80
0.00 C 270.29 1.10 269.84 2.22 269.41 3.34 C
270.05 3.42 271.34 3.57 271.98 3.65 C 271.83
2.43 271.66 1.21 271.49 0.00 L 320.83 0.00 C
320.62 1.16 320.43 2.32 320.27 3.48 C 320.88
3.49 322.11 3.50 322.73 3.51 C 322.60 2.64
322.35 0.89 322.23 0.01....
Compression
How much wood could
a woodchuck chuck if a
woodchuck could chuck wood?
Compression
How much wood could
a woodchuck chuck if a
woodchuck could chuck wood?
wood = 1 could = 2 chuck = 3
Compression
How much wood could
a woodchuck chuck if a
woodchuck could chuck wood?
wood = 1 could = 2 chuck = 3
How much 1 2 a 13 3 if a 13 2 3 1?
Assignments
- Read and be prepared to discuss:
- Pattern on the Stone Chapter 7: Speed: Parallel Computers
- Blog 2: Algorithms - Due Monday 9/19 10:00 PM
- Scratch Sorting Project - Due 9/20 10:00 PM
Blog 2: Algorithms
There are many important algorithms in Computing Science. In fact, we’re going to learn about many of them later in this class. For now, however, I’d like you to pick an algorithm from Wikipedia’s list of algorithms (https://en.wikipedia.org/wiki/List_of_algorithms) and write about it. Some things you can cover:
- Where did this algorithm come from?
- How does it work?
- What makes it special or unique?
- Are there other algorithms that achieve the same or similar outcome?
- Could you do this algorithm manually? Or does it require a computer?
- How does this algorithm relate to what we’ve already read in the textbook? Did the textbook help you understand how this algorithm works? (textbook references)
- Where can this algorithm be found in the real world? (outside reference)
Binary Worksheet