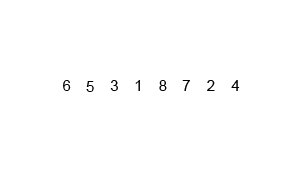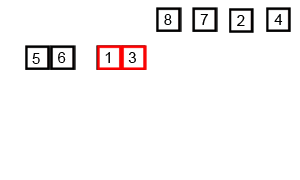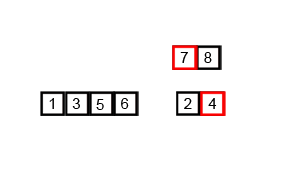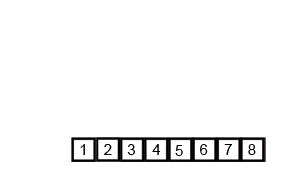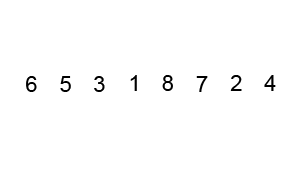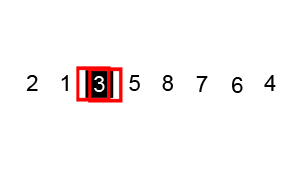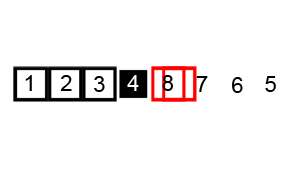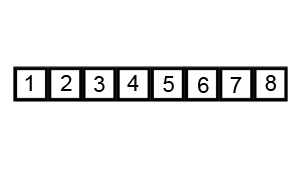CIS 115

Algorithms

al-Khwārizmī

Abū ʿAbdallāh Muḥammad ibn Mūsā al-Khwārizmī

Image Source: Wikipedia

Algorithm

A finite list of specific instructions for carrying out a procedure or solving a problem

Euclid

Image Source: Wikipedia

Euclid's Algorithm (GCD)

1. Start with 2 numbers, A and B
2. If either one is zero, the answer is the other number
3. Subtract the smaller number from the larger number
4. Repeat steps 2 - 4 until an answer is found

Example: GCD of 1071 & 462

Example: GCD of 1071 & 462

• 1071, 462
• 609, 462
• 147, 462
• 147, 315
• 147, 168
• 147, 21
• 126, 21
• 105, 21
• 84, 21
• 63, 21
• 42, 21
• 21, 21
• 21, 0
• 21

Sorting Algorithms

• Insertion Sort
• Bubble Sort
• Merge Sort
• Quicksort

Insertion Sort

Image Source: Wikipedia

1. Choose an element from the source
2. Place it in the correct place in the destination
3. Repeat until source is emtpy

Bubble Sort

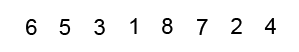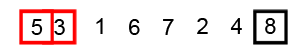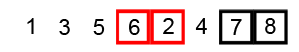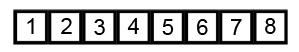
Image Source: Wikipedia

1. Compare the first two elements
2. If they are out order, swap them
3. Move one element over and repeat
4. When the end is reached, start over
5. Continue until no more swaps are made

Big O Notation

Image Source: Wikipedia

Big O Notation

• A way to express the complexity of an algorithm
• Approximates the number of steps needed based on the size of the input
• Assumes the input is a "worst case" input

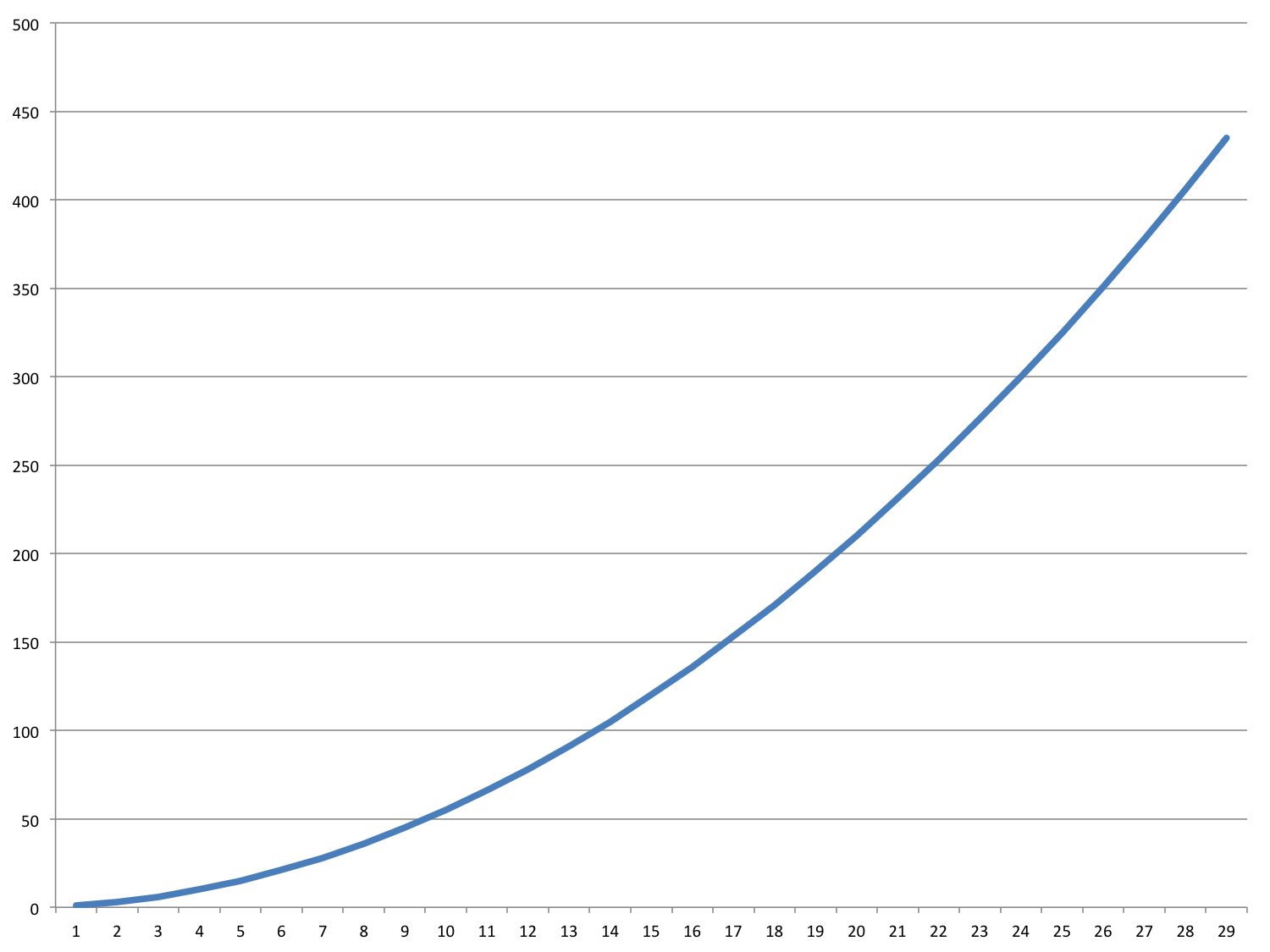
Bubble Sort - Worst Case?

• 3, 2, 5, 4, 7, 6, 9, 8, J, 10, K, Q, A
• A, 2, K, 3, Q, 4, J, 5, 10, 6, 9, 7, 8
• A, Q, K, 10, J, 8, 9, 6, 7, 4, 5, 3, 2
• A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2
• 2, 4, 6, 8, 10, Q, A, 3, 5, 7, 9, J, K

Bubble Sort - Worst Case?

• 3, 2, 5, 4, 7, 6, 9, 8, J, 10, K, Q, A - 6
• A, 2, K, 3, Q, 4, J, 5, 10, 6, 9, 7, 8 - 42
• A, Q, K, 10, J, 8, 9, 6, 7, 4, 5, 3, 2 - 73
• A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2 - 78
• 2, 4, 6, 8, 10, Q, A, 3, 5, 7, 9, J, K - 21

Bubble Sort - Worst Case?

Sorting Algorithms

• Insertion Sort - O(n²)
• Bubble Sort - O(n²)
• Merge Sort
• Quicksort

Merge Sort

Image Source: Wikipedia

Merge Sort

1. Split the items into two halves
2. Repeat step 1 until each has 1 item
3. Choose 2 parts and merge them together by choosing the smallest item repeatedly from the front of each part
4. Continue merging parts together until no more remain

Quicksort

Image Source: Wikipedia

Quicksort

1. Choose an item from the list as a "pivot"
2. Put all items less than that item to its left, and put all items greater to its right
3. Repeat these steps for the items on each side of the pivot.

Sorting Algorithms

• Insertion Sort - O(n²)
• Bubble Sort - O(n²)
• Merge Sort - O(n log n)
• Quicksort - O(n²) - avg. O(n log n)

Everyday Heuristics

• Rule of Thumb
• Educated Guess
• Common Sense
• Try something and work backwards
• Do a simpler problem first

Traveling Salesman Problem

Image Source: Wikipedia

Traveling Salesman Problem: Algorithms

• Brute Force - O(n!)
  • Easy & Cheap, but not fast
  • 8 cities = 40320 steps
• Dynamic Programming - O(2ⁿ)
  • Faster, but not easy or cheap
  • 8 cities = 256 steps

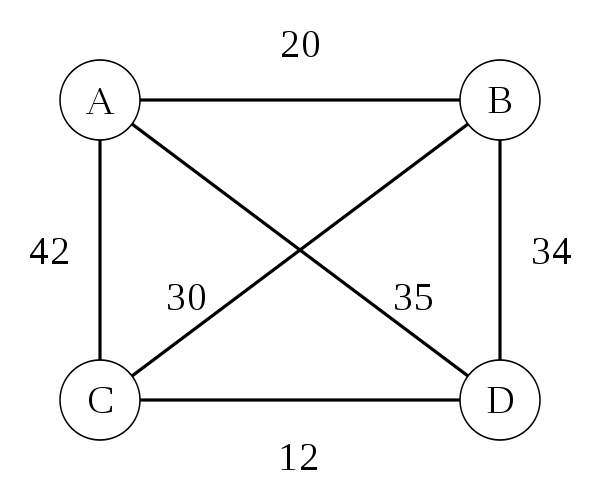
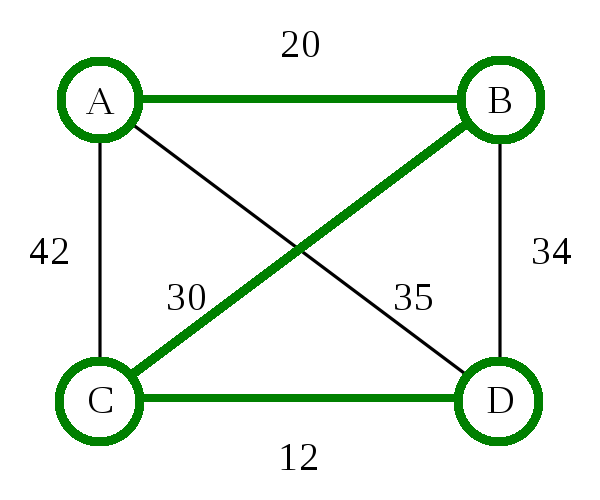
Traveling Salesman Problem: Heuristic

Nearest Neighbor (Greedy Algorithm)

• Pick any city (we'll use B)
• Go to the closest city you haven't been to yet
• From that city, repeat this process until all cities have been visited

Traveling Salesman Problem

Greedy Solution: 67 miles

Image Source: Wikipedia

Traveling Salesman Problem

Optimal Solution: 62 miles

Image Source: Wikipedia

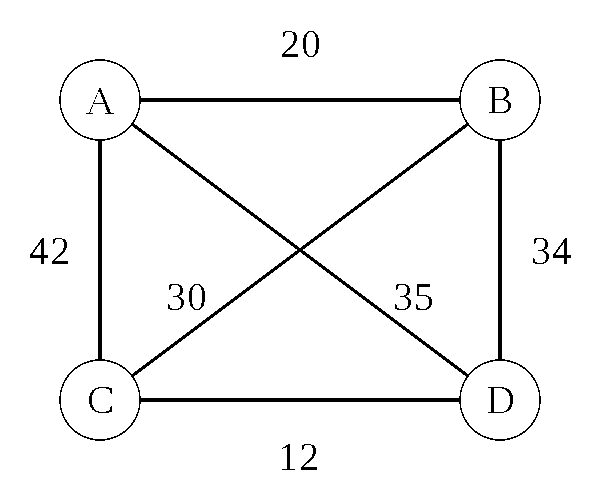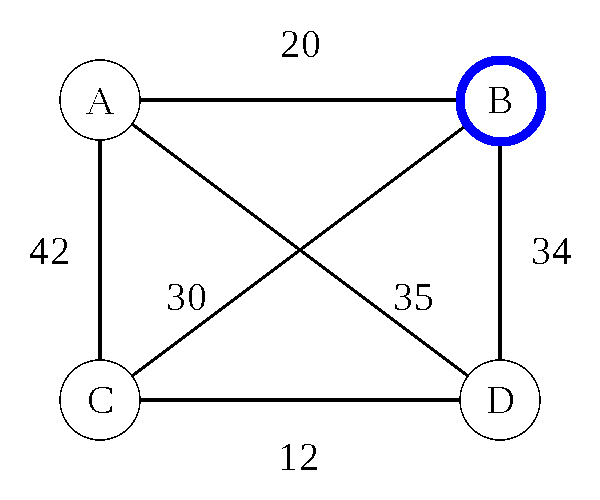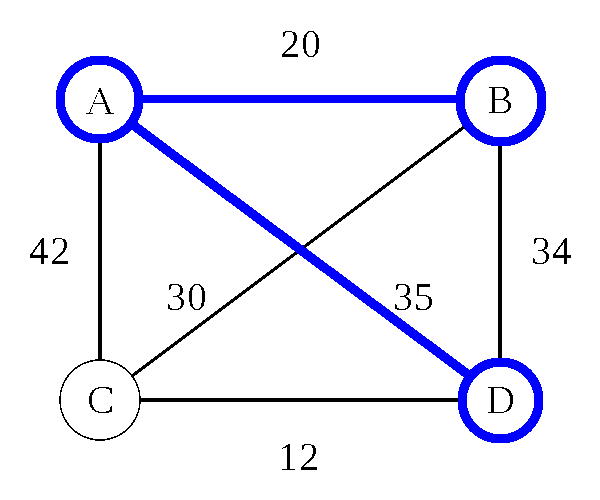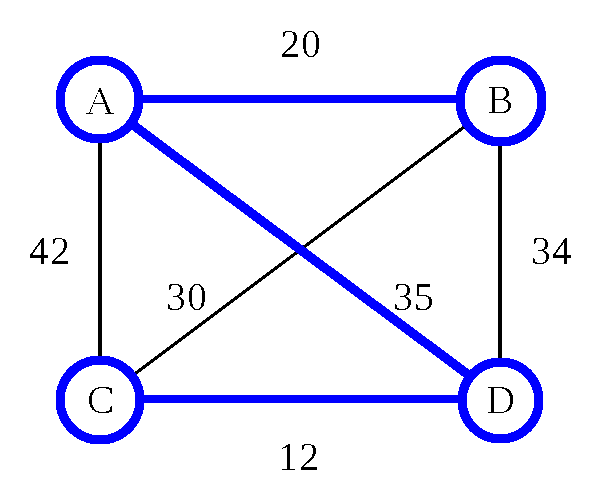
Traveling Salesman Problem: Heuristic

Nearest Neighbor (Greedy Algorithm) - O(d n)

• d is the number of dimensions
• n is the number of cities
• 8 cities = 16 steps (assuming 2D maps)

Time can vary widely based on how the data is presented and sorted

Assignments

• Read and be prepared to discuss:
  • Pattern on the Stone Chapter 6: Memory: Information and Secret Codes
• Blog 3: Algorithms -
  Due Monday 9/21 10:00 PM
• Scratch Sorting Project -
  Due 9/22 10:00 PM

Blog 3: Algorithms

Think about something that you do every day. That one thing probably is composed of many smaller steps, which you have to perform in the correct order. How would you describe those steps to someone unfamiliar with the action? How would you describe them to a robot that can follow your actions? While we may not think of it in this way very often, most of our daily lives could be expressed as an algorithm. Choose a few examples of actions you perform often, and write about how you would express them as algorithms. Some things to consider:

• Could a computer system be built to follow this algorithm easily?
• Are there algorithms you perform daily that would be very difficult for a computer?
• Is the algorithm you use the fastest one? Are there real-world limitations that prevent you from doing it faster?
• If the algorithm you use the most efficient one (the least number of steps) or simply the one that you learned first?
• How do you share your “algorithms” with others so they can follow along?

Bubble Sort

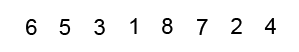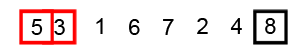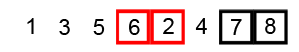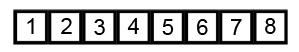
Image Source: Wikipedia

1. Compare the first two elements
2. If they are out order, swap them
3. Move one element over and repeat
4. When the end is reached, start over
5. Repeat these steps as many times as the number of items in the list