CIS 115
Lecture 17: Cryptography
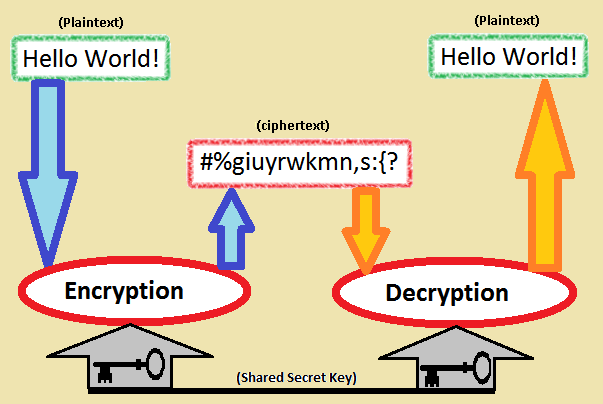
Cryptography
- Study of ways to communicate securely and privately in the presence of third parties
- Charles Babbage, Edgar Allan Poe, Alan Turing, and Claude Shannon were all involved in cryptography.
Message to the Class
TSTEPHAAXLISLAESCEMQIYQMessage to the Class
TSTEPHAAXLISLAESCEMQIYQT H I S I S A S C Y T A L E Q E X A M P L E QEarly Ciphers
- Substitution Ciphers
- Cryptoquip - Easily Breakable
- Polyalphabetic Ciphers
- First described by Al-Kindi in the 9th century
- Later explained by Leon Battista Alberti in 1467
Image Source: Wikipedia

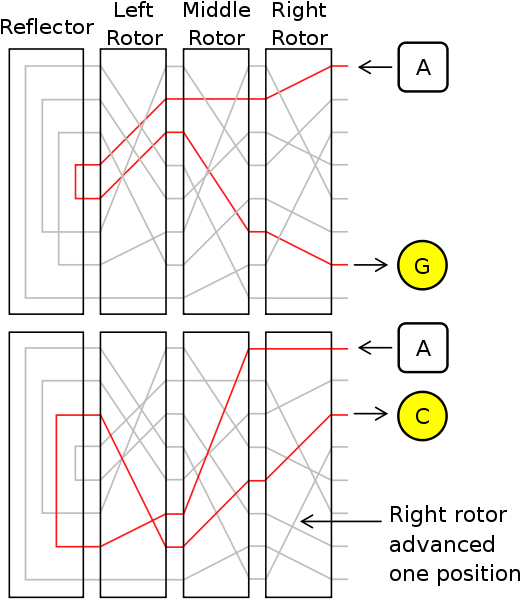
Image Source: Wikipedia
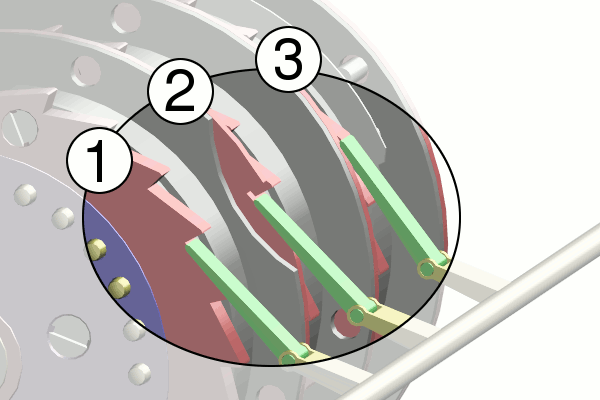
Enigma Key
- Choice and order of rotors
- Initial position of rotors
- Ring setting on rotors
- Plug connections
Enigma Operation
- Set wheels to today's key from codebook
- Operator chooses message key
- Encode message key TWICE to avoid errors
- Set wheels to message key
- Encrypt and send message
Enigma Stengths
- Many factors to the encryption
- Had up to 8 different wheels to choose from by the end of the war
- 150 Trillion different setups
Enigma Weaknesses
- A letter would never encrypt to itself
- Plugboards were reciprocal
- Wheels were not similar enough (could determine which wheels were used)
- Poor policies and procedures
Cracking Enigma
- 1932 - First cracked by Marian Rejewski of Poland
- 1938 - Germany added 2 wheels
- 1939 - Alan Turing creates Bombe
- 1945 - Almost every message deciphered within 2 days
Impact
“My own conclusion is that it shortened the war by not less than two years and probably by four years … we wouldn't in fact have been able to do the Normandy Landings, even if we had left the Mediterranean aside, until at the earliest 1946, probably a bit later.”
-Sir Harry Hinsley
British Intelligence Historian
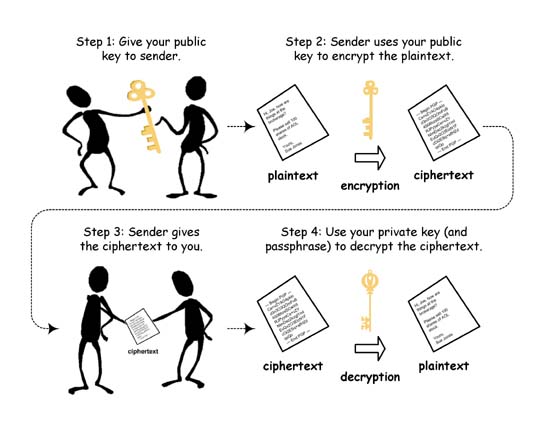
RSA Encryption
- Developed in 1977
- Named for the 3 creators (Ron Rivest, Adi Shamir, Lenonard Adleman)
- Uses the product of 2 large prime numbers to generate a key
- Key strength depends on the difficulty of factoring large numbers
RSA Example
- Choose 2 distinct prime numbers
p and q - Compute their product n = pq
- Compute the totient t of n:
t = (p - 1)(q - 1)
RSA Example
- Choose any number e less than t that is coprime to t (they share no common factors but 1)
- Calculate d as the modular multiplicative inverse of e (mod t)
e * x = 1 (mod t)
RSA Keys
- Public Key : (n, e)
- Encode: c = me (mod n)
- Private Key : (n, d)
- Decode: m = cd (mod n)
Assignments
- Read and be prepared to discuss:
- Tubes Chapter 7: Where Data Sleeps
- Blog 8: TBD - Due 10/27 10:00 PM
- HTML & CSS Project - Due 10/21 10:00 PM
- Scratch Chaocipher - Due 10/28 10:00 PM
Blog 8: TBD
TBD
- TBD
RSA Activity
- Fill out the RSA Activity Worksheet